根据 AISC 360-22 (LRFD, ASD)进行验算
受剪验算
钢骨混凝土组合截面的抗剪计算保守地转化为 钢结构截面强度验算.
抗剪强度:
![]()
其中: | Av | - | 钢截面剪切面积,对于圆形截面等于 2As / π |
Fy | - | 选用钢材的规定最小屈服应力 | |
Kc | - | 保守取 1.0 | |
Ac | - | 混凝土面积 | |
fc' | - | 选用混凝土的规定最小抗压强度 |
抗剪验算时:
- 采用 LRFD: Q / (Vn ϕv ) ≤ 1.0
- 采用 ASD: Q / (Vn / Ωv ) ≤ 1.0
受压验算
抗压强度:
![]()
"紧凑型"圆形HSS充填混凝土后的抗压强度:
![]()
其中: | As | - | 钢材截面面积 |
Ac | - | 混凝土截面面积 |
"非紧凑型"圆形HSS充填混凝土后的抗压强度:
![]()
![]()
其中: | λp, λr | - | 截面高厚比,参照 AISC 360 and Tab.I1.1a |
λ | - | 高厚比 = D / t | |
D | - | 圆形HSS外径 | |
t | - | 圆形HSS厚度 |
"纤细"圆形HSS充填混凝土后的抗压强度:
![]()
其中: | Fn | - | 临界屈曲应力 |
![]()
其中: | Es | - | 钢的弹性模量 |
许用抗压强度:
- 采用 LRFD: Pc = Pn ϕc
- 采用 ASD: Pc = Pn / Ωc
受弯验算
抗弯验算时,采用弯矩影响下的法向应力分布结合相应的作用图解。
钢骨混凝土组合截面的抗弯验算时,假定的法向应力分布形式如下图所示:
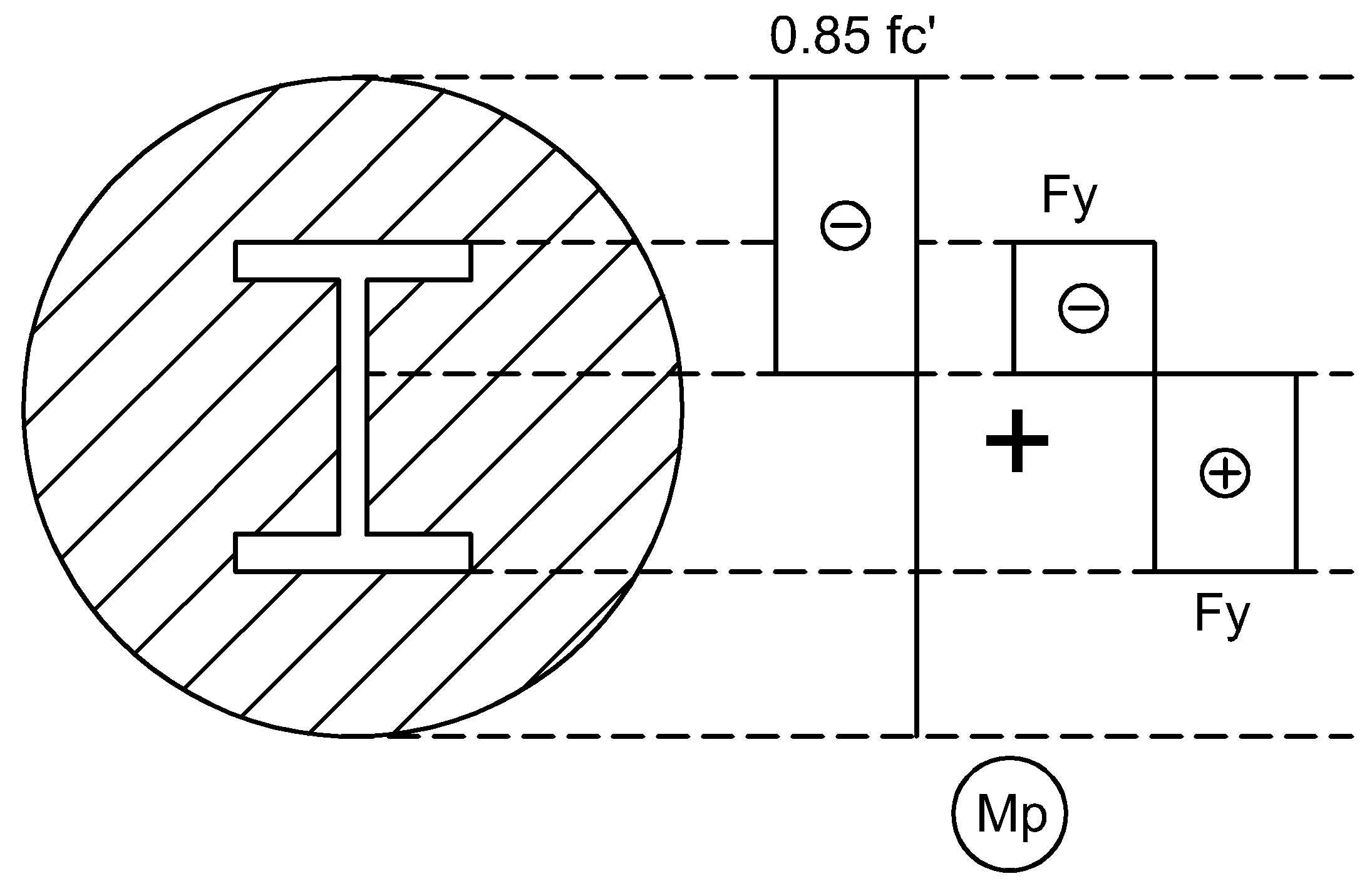
抗弯强度公式:
![]()
其中: | Mp | - | 复合截面塑性应力分布对应的力矩 |
对圆形HSS充填混凝土的截面,法向应力的假定分布形式取决于 D/t :
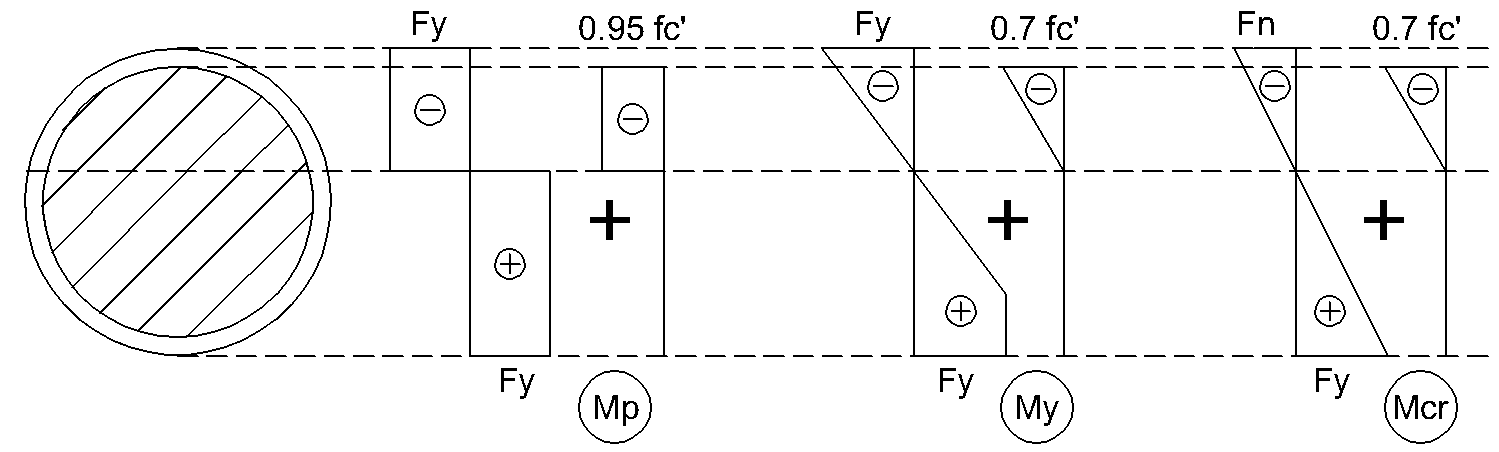
"紧凑型"圆形HSS充填混凝土后的抗弯强度:
![]()
"非紧凑型"圆形HSS充填混凝土后的抗弯强度:
![]()
其中: | My | - | 截面弹塑性应力分布时对应的屈服力矩 |
λp, λr | - | 截面高厚比,参照AISC 360 Table I1.1b |
"纤细"圆形HSS充填混凝土后的抗弯强度:
![]()
其中: | Mcr | - | 截面弹塑性应力分布时对应的第一屈服力矩 |
许用抗弯强度:
- 采用 LRFD: Mcx = Mn ϕb
- 采用 ASD: Mcx = Mn / Ωb
压弯验算
压弯验算计算公式:
- 当: N / Pc ≥ 0.2
![]()
- 当: N / Pc < 0.2
![]()